Machine learning: presentiamo brevemente alcuni modelli per l’integrazione di machine learning per lo studio di time series.
Il Machine Learning negli ultimi anni si è molto affermato, grazie alla crescita della potenza di calcolo e della capacità di parallelizzazione delle operazioni offerte da strumenti come le GPU e le varie derivazioni (ad esempio, le TPU).
Questo articolo è una prosecuzione della serie iniziata con Analisi di Time Series, Parte 1.
Machine Learning e Time Series
Prevedere lo sviluppo futuro di una time series può essere un compito piuttosto complicato e impreciso, soprattutto in quegli ambiti dove il fenomeno registrato nella time series è soggetto a oscillazioni casuali o le cui cause sono sconosciute e difficilmente analizzabili. Recentemente, però, l’utilizzo di metodi di Machine Learning nell’ambito del time series forecasting ha permesso di ottenere risultati interessanti, soprattutto per quel che riguarda le previsioni a breve termine. Presentiamo nel prossimo paragrafo una classe di modelli di Machine Learning: le reti neurali ricorrenti.
Neural Network e Time Series
Le reti neurali hanno dimostrato buoni risultati nelle applicazioni in vari campi. Uno di questi è la previsione di valori futuri di una time series.
Il più semplice modello di rete neurale è una feedforward, fully connected neural network. Ciò significa che la rete neurale processa dati in una sola direzione, dall’input all’output, senza retroazione; inoltre, ciascuna unità (detta anche “neurone”) di ciascun livello è connessa ad ogni unità del livello seguente (e di quello precedente).

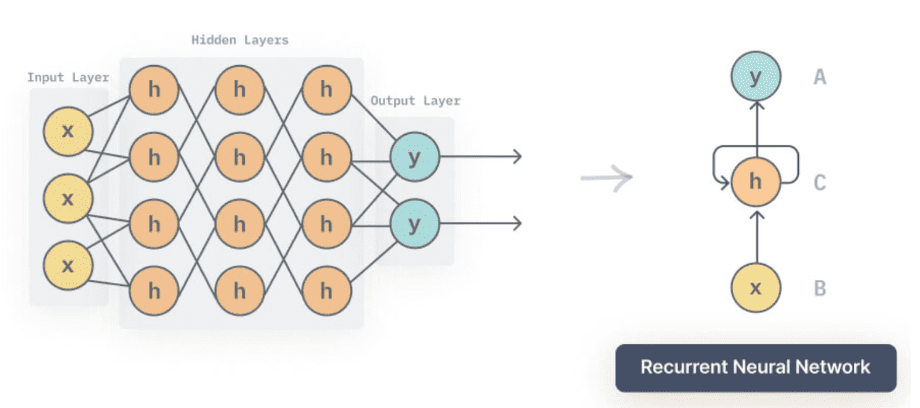
Nell’esempio dell’immagine precedente vediamo una rete neurale formata dal livello di input (in viola), due livelli nascosti (quelli formati dalle unità in verde) e un livello di output. In questo esempio si ha a che fare con un problema di classificazione: il modello riceve quattro valori in input e produce in output tre valori, che rappresentano in qualche modo la classe prevista per l’input.
Un siffatto tipo di rete neurale non si presta all’utilizzo nel campo delle time series: ciò è dovuto al fatto che la rete neurale riceve tutti gli input a un dato tempo (iniziale), non è quindi in grado di analizzare le proprietà di una sequenza.
Un’architettura più adatta all’analisi di time series è quella fornita dalle reti neurali ricorrenti, per le quali lo stato della rete ad un certo punto dell’elaborazione può influire sulle elaborazioni seguenti.

Nella figura precedente vediamo come, in una rete neurale ricorrente, vi sia un qualche tipo di auto-azione, di auto-feedback delle unità “su se stesse”: questa caratteristica permette di adattare le reti neurali ricorrenti all’analisi di time series.
Le reti neurali ricorrenti, però, presentano alcuni problemi legati alla difficoltà di training, in particolare il vanishing/exploding gradient problem. Non ci vogliamo addentrare qui nella presentazione di questa problematica, basti dire che vi sono modelli di reti neurali che permettono di evitare tale inconveniente: le Long-Short Term Memory network (LSTM) e i Gated Recurrent Unit (GRU).
Da un punto di vista pratico, è molto semplice predisporre una rete neurale che, dati n step di una time series, preveda il valore al tempo successivo. A tal fine, bisogna predisporre la sequenza di dati di training della rete in modo che il problema sia trasformabile in un supervised learning. Supponiamo che la nostra time series sia data dalla sequenza di dati:
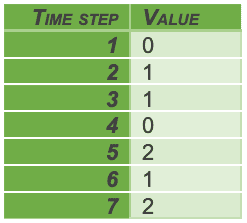
Supponiamo inoltre di voler addestrare la nostra rete a prevedere il prossimo valore dalla sequenza dei tre valori precedenti. Predisponiamo quindi una tabella dove associamo ad ogni dato la sequenza dei tre dati precedenti:

Dividiamo quindi i nostri dati in due parti: i dati di test, X_test e y_test, e i dati di training, X_train e y_train. Ignoriamo per il momento il problema della validazione, immaginando di utilizzare degli iperparametri fissati (il numero di unità, l’optimizer, la funzione loss, …). Inoltre, immaginiamo di aver già normalizzato i dati (ad esempio, usando un sklearn.preprocessing.MinMaxScaler.
Definiamo una rete LSTM usando keras:
lstm = Sequential()
lstm.add(
LSTM(
50,
return_sequences=False)
)
lstm.add(Dense(1))
Procediamo poi alla fase di compile:
lstm.compile(
optimizer=”adam”,
loss=”mean_squared_error”,
metrics=[“accuracy”]
)
Infine, eseguiamo il fit della rete:
lstm.fit(
X_train,
y_train,
batch_size=1,
epochs=10
)
lstm.summary()
A questo punto, possiamo usare la rete per eseguire delle previsioni sui dati di test e valutare la performance:
y_hat = lstm.predict(X_test)
Una rete simile potrebbe produrre delle previsioni come quelle nell’immagine seguente:

Va ricordato che la rete prevede per ogni sequenza di step solamente il valore successivo: è un caso di single-step prevision.
Un esempio concreto: potremmo voler prevedere il valore di un titolo di borsa dato lo storico dei valori nei tre giorni precedenti. Questo modello non ci permette di eseguire previsioni a lungo termine, ma si può rivelare molto utile per il trading a breve termine.
Un altro esempio, proveniente dal mondo industriale, potrebbe essere la previsione di una misurazione di temperatura (media) per un’unità di tempo (diciamo un’ora) successiva basata sulle temperature delle tre ore precedenti.
Previsioni Multi-Step
La previsione di più step temporali è un problema più complesso. La rete neurale deve tentare di estrapolare un modello che rappresenti la dinamica di qualche step del fenomeno, il che, in alcuni casi, si rivela davvero complicato. Spesso, simili previsioni multi-step presentano tassi di errore piuttosto che crescono man mano che si procede con gli step: l’errore al giorno successivo sarà probabilmente inferiore all’errore al giorno n+2.
Conclusioni
In questo articolo abbiamo presentato qualche idea di come si possano utilizzare neural network per studiare e prevedere il comportamento futuro di time series.
Non c’è bisogno di sottolineare che qui ci siamo limitati ai concetti essenziali; le tecniche utilizzate in progetti reali sono oggigiorno molto più complesse e richiedono familiarità con algoritmi più complessi di quelli qui menzionati.


